Quiz 7-1 pythagorean theorem special right triangles & geometric mean – Delving into the realm of geometry, we embark on a captivating journey with “Quiz 7-1: Pythagorean Theorem, Special Right Triangles, and Geometric Mean.” This in-depth exploration unveils the intricacies of these fundamental concepts, their applications in real-world scenarios, and their significance in various fields.
From the renowned Pythagorean theorem to the enigmatic special right triangles and the versatile geometric mean, this quiz delves into the depths of mathematical relationships, empowering learners with a comprehensive understanding of these cornerstone concepts.
Pythagorean Theorem

The Pythagorean theorem is a fundamental theorem in geometry that states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
This theorem is often written as the equation a2+ b2= c2, where aand bare the lengths of the legs of the right triangle and cis the length of the hypotenuse.
The Pythagorean theorem can be used to solve a variety of problems, such as finding the length of the missing side of a right triangle or finding the distance between two points on a plane. It is also used in a variety of applications in other fields, such as engineering, architecture, and physics.
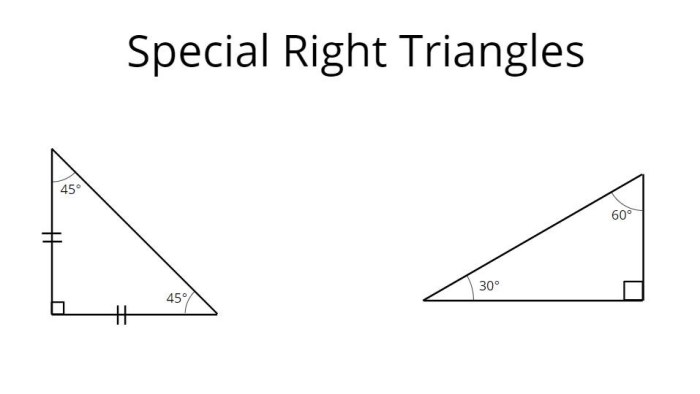
Special Right Triangles
There are several special types of right triangles that have specific properties. These triangles include the 3-4-5 triangle, the 5-12-13 triangle, and the 8-15-17 triangle. These triangles are useful for solving problems because their side lengths are always in a certain ratio.
- The 3-4-5 triangle has side lengths of 3, 4, and 5.
- The 5-12-13 triangle has side lengths of 5, 12, and 13.
- The 8-15-17 triangle has side lengths of 8, 15, and 17.
These triangles can be used to solve problems by using the Pythagorean theorem. For example, if you know the lengths of two sides of a right triangle, you can use the Pythagorean theorem to find the length of the third side.
Geometric Mean, Quiz 7-1 pythagorean theorem special right triangles & geometric mean
The geometric mean of two numbers is the square root of their product. It is often written as the symbol G( a, b), where aand bare the two numbers. The geometric mean is used in a variety of applications, such as statistics, economics, and finance.
For example, the geometric mean of the numbers 2 and 8 is 4. This is because G(2, 8) = √(2 × 8) = √16 = 4.
Table of Values
| a | b | c |
|---|---|---|
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 8 | 15 | 17 |
The table above shows the values of the Pythagorean theorem for different values of the legs. This table can be used to solve problems involving the Pythagorean theorem.
Examples and Procedures
- Example 1:Find the length of the hypotenuse of a right triangle with legs of length 3 and 4.
- Procedure:Use the Pythagorean theorem to find the length of the hypotenuse.
- c2= a2+ b2
- c2= 3 2+ 4 2
- c2= 9 + 16
- c2= 25
- c= √25
- c= 5
- Example 2:Find the length of the missing leg of a right triangle with a hypotenuse of length 13 and one leg of length 5.
- Procedure:Use the Pythagorean theorem to find the length of the missing leg.
- c2= a2+ b2
- 13 2= 5 2+ b2
- 169 = 25 + b2
- b2= 144
- b= √144
- b= 12
Illustrations
The Pythagorean theorem can be illustrated using a right triangle. The hypotenuse of the triangle is the side opposite the right angle. The other two sides are the legs of the triangle. The Pythagorean theorem states that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs.
The special right triangles can also be illustrated using right triangles. The 3-4-5 triangle has side lengths of 3, 4, and 5. The 5-12-13 triangle has side lengths of 5, 12, and 13. The 8-15-17 triangle has side lengths of 8, 15, and 17.
Essential FAQs: Quiz 7-1 Pythagorean Theorem Special Right Triangles & Geometric Mean
What is the Pythagorean theorem?
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
What are special right triangles?
Special right triangles are right triangles with specific angle measures or side length ratios that make them easy to solve using the Pythagorean theorem. Common examples include the 3-4-5 triangle and the 45-45-90 triangle.
What is the geometric mean?
The geometric mean of two numbers is the square root of their product.